




 In this page:
Worked Example 1
|
In this example, I am going to
introduce 5 strategies: (1) Use a Diagram
(2) Make a Supposition
(3) Use a "Before-and-After" Comparison
(4) Use an Equation
(5) Use Ratio
Worked Example 1
Extracted from Maths.
Textbook, Pg. 15, Ex 1D, Q1.
Mr. Fu bought 2 identical television sets.
He sold one at a profit of 25% and the other at the loss of 25%. Upon the sale of the
television sets, did he gain, make a loss or break even?
2 Television Sets
125% (1st Television Set)
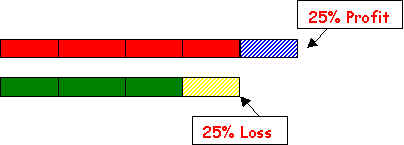
75% (2nd Television Set)
Suppose that the price of both television sets are made up
of four equal parts each. For the first television set, when it is sold at 25% profit,
there will be 5 equal parts altogether. For the second television set, when it sold at 25%
loss, there will only be 3 equal parts left.
Before, there were 8 equal parts. After that, there are
still 8 equal parts. Therefore, Mr. Fu did not make a gain or loss. He broke even.
Suppose the cost price of the television sets is $100 each.
For the first television set, it is sold at = 125% x
$100 = $125 For the second television set, it is sold at = 75% x $100 = $75
Their cost prices are $200.
The
total amount of money Mr. Fu received is = $125 + $75
= $200 Therefore, Mr. Fu did not make a gain or
loss.
 | Strategy 3: Use an Equation Let the cost prices of the 2 television sets = $2y
The
price of the first television set = 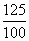 x $y = $1.25y
The price of the
second television set = x $y = $1.25y
The price of the
second television set = 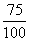 x $y = $0.75y
The selling prices of the 2 television sets = $1.25y + $0.75y = $2y x $y = $0.75y
The selling prices of the 2 television sets = $1.25y + $0.75y = $2y
The selling prices of the 2 television sets ($2y)
= The cost prices of the 2 television sets ($2y)
Therefore, Mr. Fu did not make a gain or loss.
|
First Part ---
The price of the first television set :
The price of the second television set = 100 : 100
Second part ---
The price of the first television set :
The price of the second television set = 75 : 125
Therefore, the first parts added together = 200 parts
Therefore, the second parts added together = 200 parts
Let's proceed to Example 2. |